Rethinking Imaginary
Introduction
The complex number system is often taught by introducing √-1.
A lot of meaning is lost in this notation. As a result, we are left wondering if imaginary numbers actually exist. The name doesn't help either.
Today, I hope to better explain the number system. No prior knowledge is required!
Visualizing Numbers
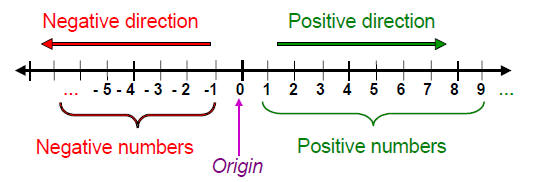
We become so accustomed to numbers that we may forget what they look like.
They live on a line. The magnitude of a number defines how far we are on the line, and the sign indicates our direction from the origin.
A 2 Dimensional Number System
In 2D, we can use a variable to describe how far we are from the origin, just like before. Let's call this the radius.
On the other hand, it is no longer possible to describe every direction by using positive and negative signs.
Instead, we will use a second variable to measure the angle of our direction from the origin.
Let's agree on the below convention for our system:
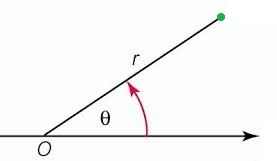
In this system, we will let the horizontal axis be the line from our 1D system.
When the angle is zero, we are on the positive side of the 1D line. When the angle is 180 degrees, we are on the negative side.
Adding
To add numbers in our system, connect lines together.
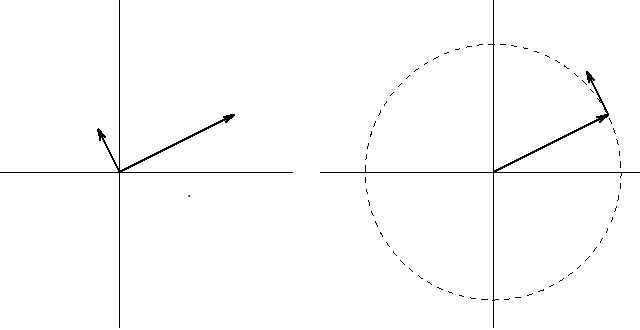
As an analogy, imagine walking in some direction for a period of time. When you decide to change directions, your final position is found by connecting your paths together.
Since the lines are not going in the same direction, the final distance from the origin is not just the sum of the length of the two lines. Instead, the result obeys laws of triangles.
Scaling
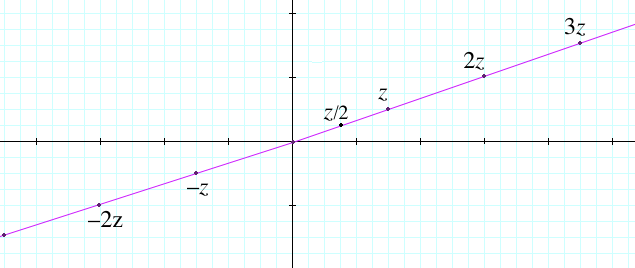
Let's take a hint from 1D.
When we want to extend (or compress) a number, we multiply it by a number:
- 5×2=10
Therefore, to scale any point, in its given direction, we will multiply by a regular number.
Rotation
Let's add rotation into our system.
With rotation at our disposal, any position is just a point on our 1D line rotated to a desired degree:
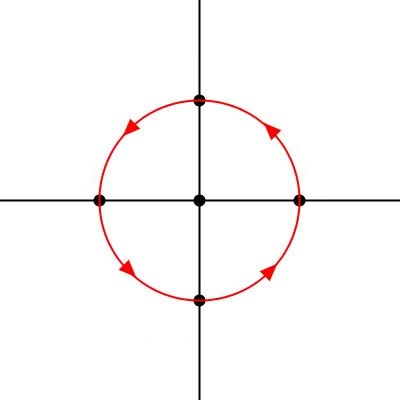
This allows us to decompose any point. For example:
- Point 1° Rotated = (Point on 1D Line)×(1° Rotation)
Consistency
It is important that rotation acts the same every time, no matter which way we are currently facing.
So we expect that repeating the rotation again would only add one extra degree:
- Point 2° Rotated = (Point on 1D Line)×(1° Rotation)2
In other words, rotations add.
Back to the Imaginary
Now we can try understand the meaning behind √-1.
If we multiply by one degree 180 times, we make a full 180 turn and end up on the negative side of the 1D line:
- Negative Point = (Positive Point)×(1° Rotation)180
A 1° rotation is not the square root of negatives. It is the 180th root!
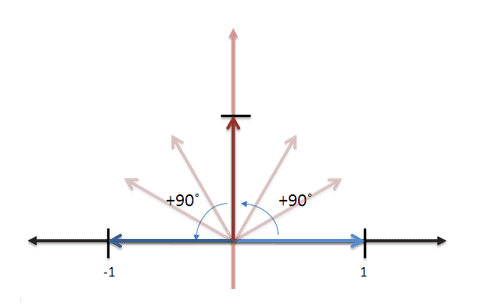
Similarly, a rotation 90 degrees from the origin could be squared to reach 180 degrees:
- Negative Point = (Positive Point)×(90° Rotation)2
Therefore, the square root of negatives in our system is a 90° rotation.
A Missing Detail
When we rotated, we used a unit for rotation, but didn't define it. Now we will solidify this idea.
Remember that when we multiply two 1D numbers, their values scale in a regular way:
- 5×2=10
Since every point can be broken down into a radius and a rotation, the product of two points can also be broken down:
- A = 10×(1° Rotation)3
- B = 5×(1° Rotation)10
Then:
- A×B = 10×(1° Rotation)3×5×(1° Rotation)10
- A×B = 50×(1° Rotation)13
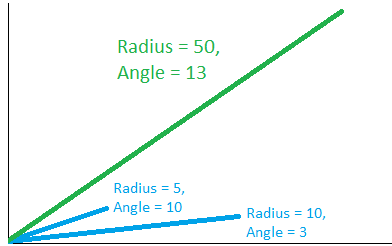
In summary, angles add and radii multiply.
Repeated Multiplication
If we multiply a number by itself over and over, we get a pattern like this, with increasingly growing radius at a steady rate of rotation.
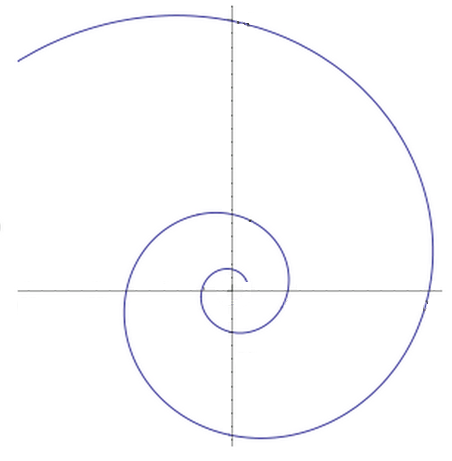
Therefore, a number purely for rotation would need a radius of 1, since angles will add up while the radius will stay at 1×1 = 1.
Similarly, 1D numbers are purely for scaling since adding an angle of zero causes no rotation.
The Square Root of Negative One
As a result of the previous section, the square root of -1 would be a point with a radius of 1 that was rotated by ninety degrees:
- 1×(90° Rotation)×1×(90° Rotation) = 1×(180° Rotation) = -1
Textbooks commonly refer to this number as i.
Our System in Nature
You might recognize the spiral from the previous section.
It turns out that our system shows up everywhere in nature:

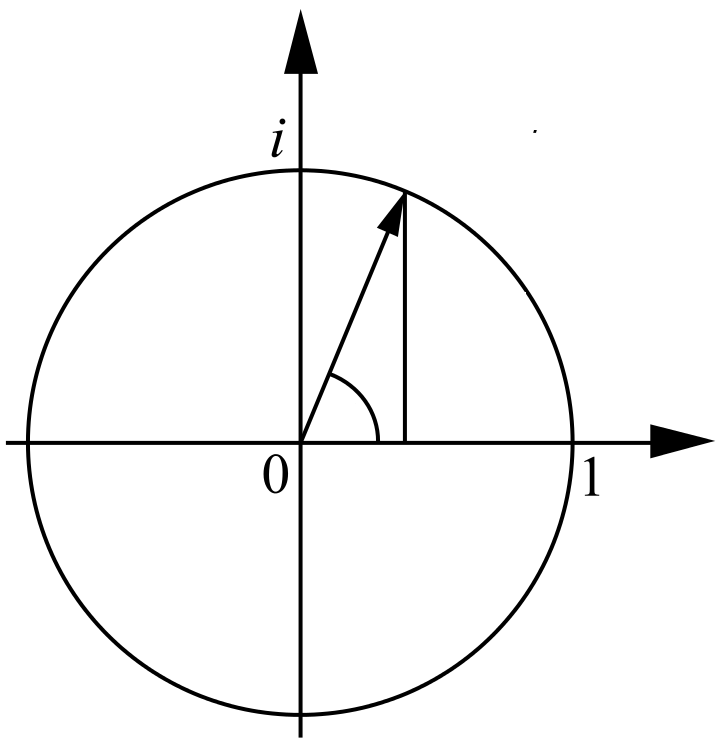
Converting to a Coordinate System
Using a radius and an angle to describe two dimensions is called a polar coordinate system.
This system has applications beyond the complex numbers since it simplifies working with circles, spirals and spheres — fundamental objects in our world.
Polar coordinates can be converted into the typical, textbook way of working with complex numbers by splitting the radius into its horizontal and vertical components.
Since we found out that i is unit length on the vertical axis, this means that any 2D point has a component that is made up of regular numbers and a component that is made up of i.
Conclusion
We now have a different view of what it means to be negative, in terms of angles rather than sign.
To find a square root of a negative, we need a new definition of multiplication which includes rotation.
With a new way to multiply, exponentiation is also redefined. Not only can exponentiation repeat multiplication, it can also repeat rotations.
All together, this makes the complex number system an excellent tool for describing phenomena in two dimensions.
Most importantly, we found out that nature is filled with complex numbers and that they are far from imaginary.

Future Work
In future posts, we will talk about the connection between complex numbers, chaos theory and fractals.
We will also learn that there is no reason to stop at 2D. The next number system, called the Quarternions, efficiently describe 3D.

Thanks for reading my first post. Your feedback and questions are appreciated!
Extra
So you might be wondering: Why do we multiply rotations to begin with?
The answer is because we chose to and it worked!
This is exactly why there is no meaning in the notation √-1.
The only way this notation works is if we decide to extend our definition of multiplication (and thus exponentiation) to include rotations.
I also said that rotations should act the same no matter where a point is. Why?
Consistency is really important when trying to introduce something new into a system. Without consistency, we wouldn't be able to predict results.
Remember, we could have taken a different direction to be the 1D line when we introduced our system. We want things to work the same no matter what convention we choose, so direction shouldn't matter!
Lastly, one detail I skipped is that numbers with a radius less than one will shrink faster and faster rather than grow:

This is just like how a number less than one gets smaller and smaller when multiplied by itself.